本文利用最近提出的比特币均衡价格模型(参见此处),结合对未来难度、产量、残差等变量的建模,对比特币未来均衡价格进行预测,并通过生成随机数残差差分对未来价格进行模拟。
限于能力,本文只对未来一个周期的行情进行预测。
自变量建模
本文用参考文章的公式(11)来对均衡价格进行预测,原式是一个截面模型,加上残差项后、该公式在时序上可表述如下:
若是想要获得的值,需要对、甚至进行建模。
标注了减半日的模型拟合效果如下:
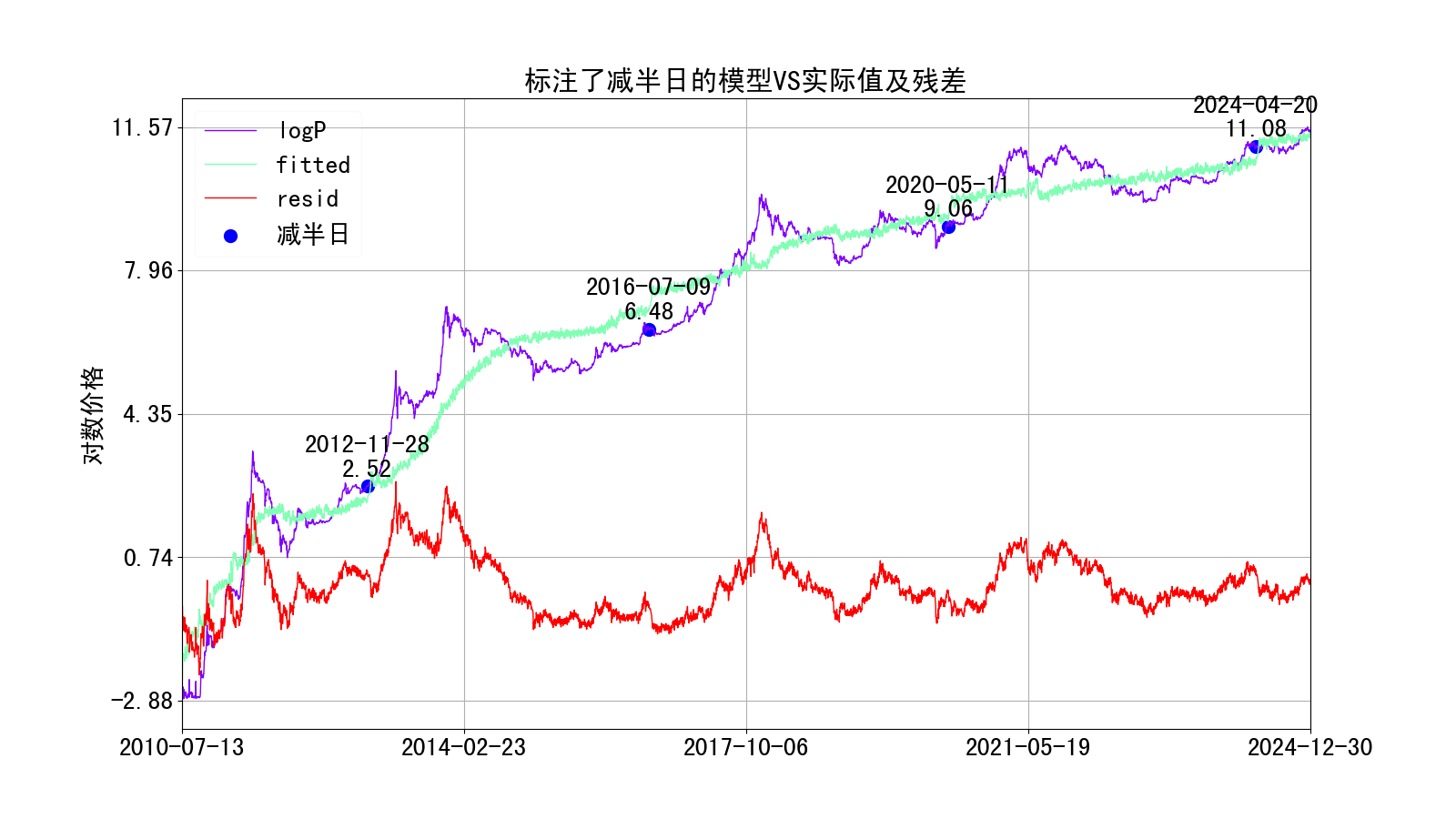
我们首先分析的特征。
由于每次减半后产量减少,可以猜测难度遵循的规律会因为减半周期不同而不同。标注出减半日的对数难度图如下:
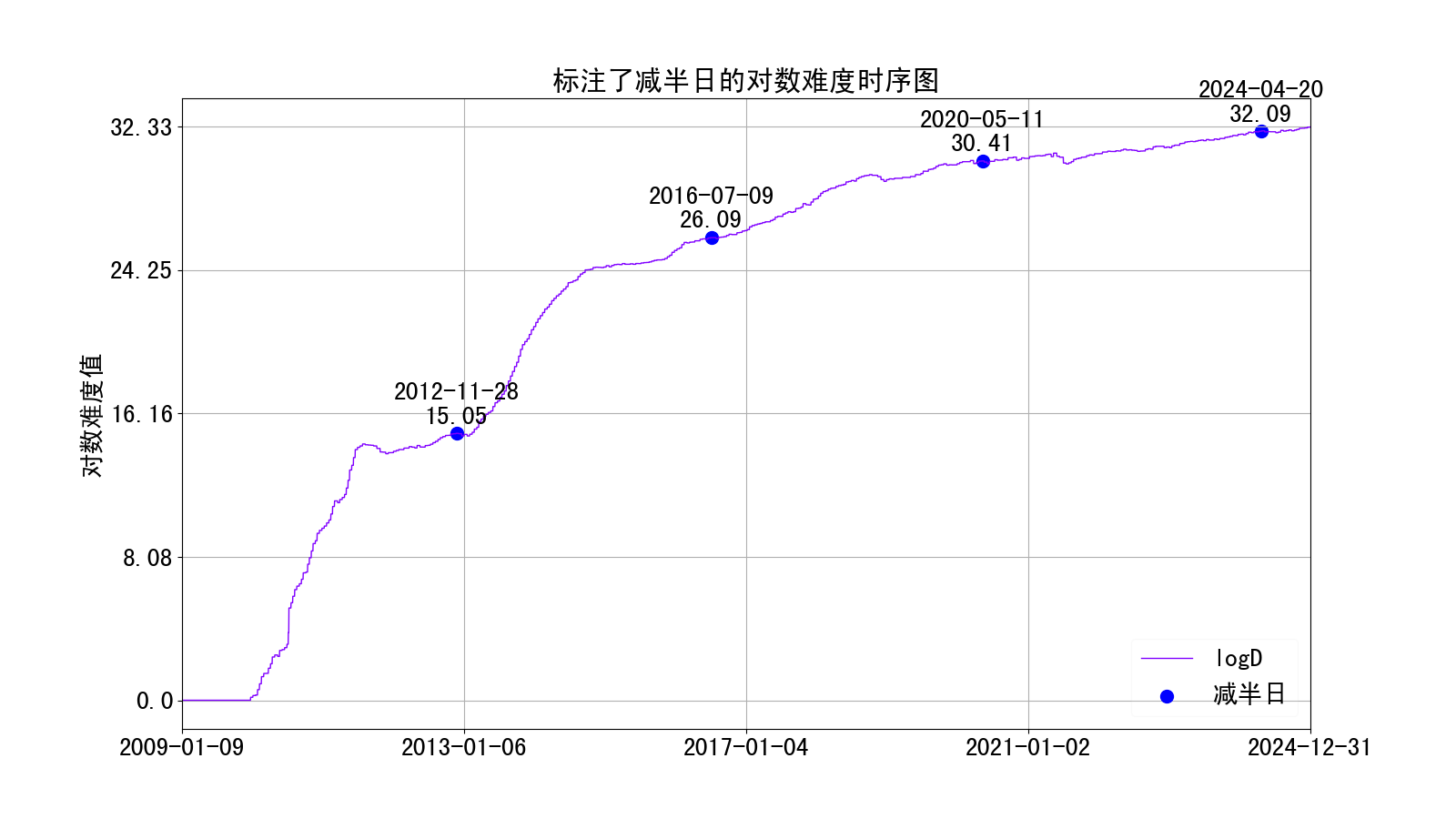
由上图可见,在较早的减半周期,对数难度变化的斜率较大、越往后斜率越小。特征如下:
- 第一次减半(对应2009.01.09-2012.11.28),对数难度先经历快速上升、后下跌、然后平稳上升直到减半日;
- 第二次减半(对应2012.11.28-2016.07.09),对数难度与第一次减半一样,也是先快速上升,后趋于平稳,然后继续上升直到减半日;
- 第三次减半(对应2016.07.09-2020.5.11),对数难度先呈线性增长,经过短期下跌,然后以新的斜率线性增长;
- 第四次减半(对应2020.05.11-2024.04.20),对数难度先呈线性增长,经过短期下跌,然后以新的斜率线性增长,新旧斜率相差不大。
如上,我们可以简单的假设第五次减半周期内(2024.04.20-约2028.03.26)对数难度以线性增长,斜率由最近的数据线性回归定出。当然,需要指出对数难度本身是一个具有随机性的数,会随着价格的上涨下跌而调整。模型只是在对其未来的可能性作简单的模拟。
作出最近一段时间的对数难度与BTC上线天数的回归图,如下:
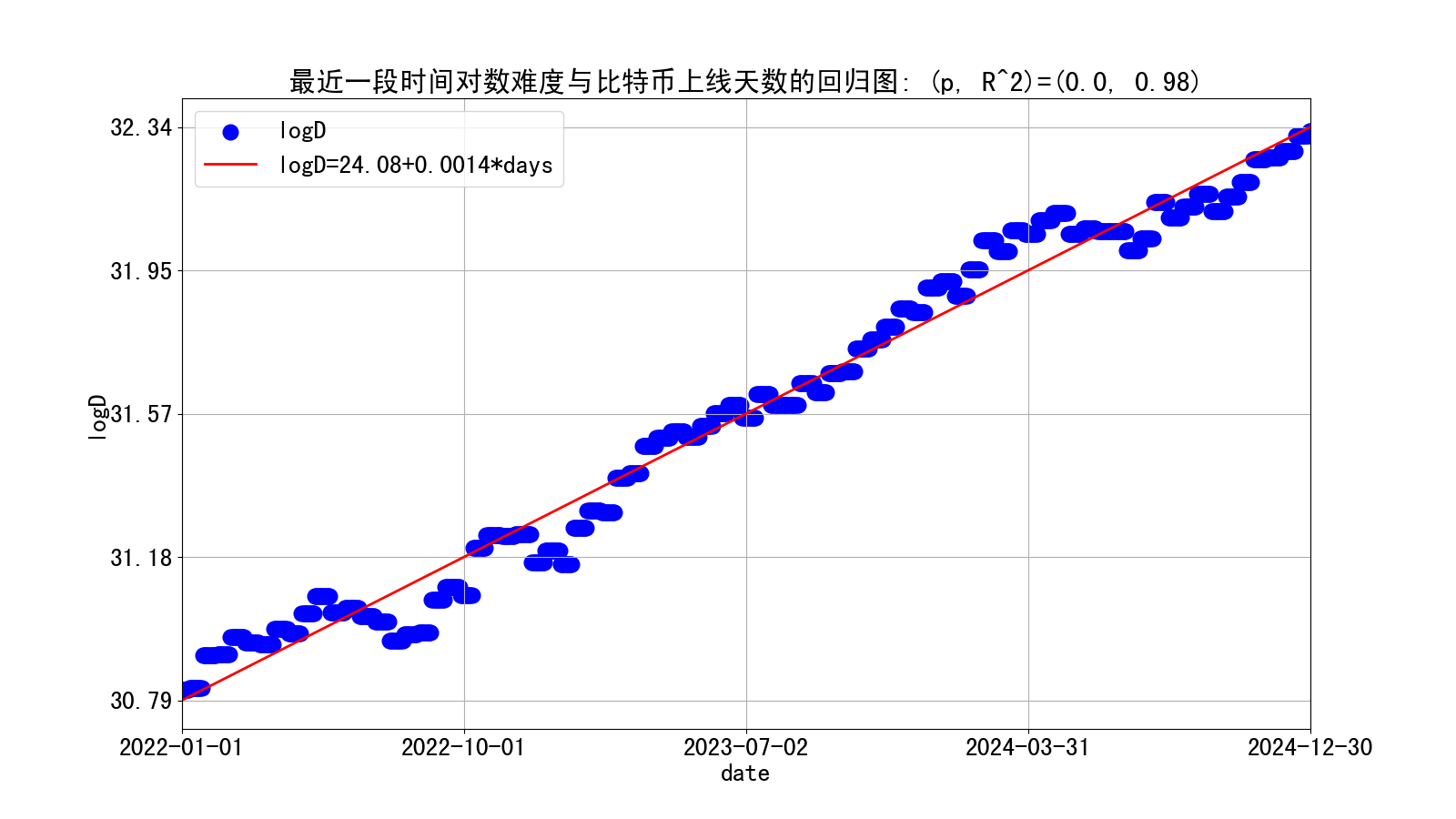
如上图所示,我们可以如下预估未来一段时间的对数难度:接着,作出标注了减半日的产量相关项图,如下:
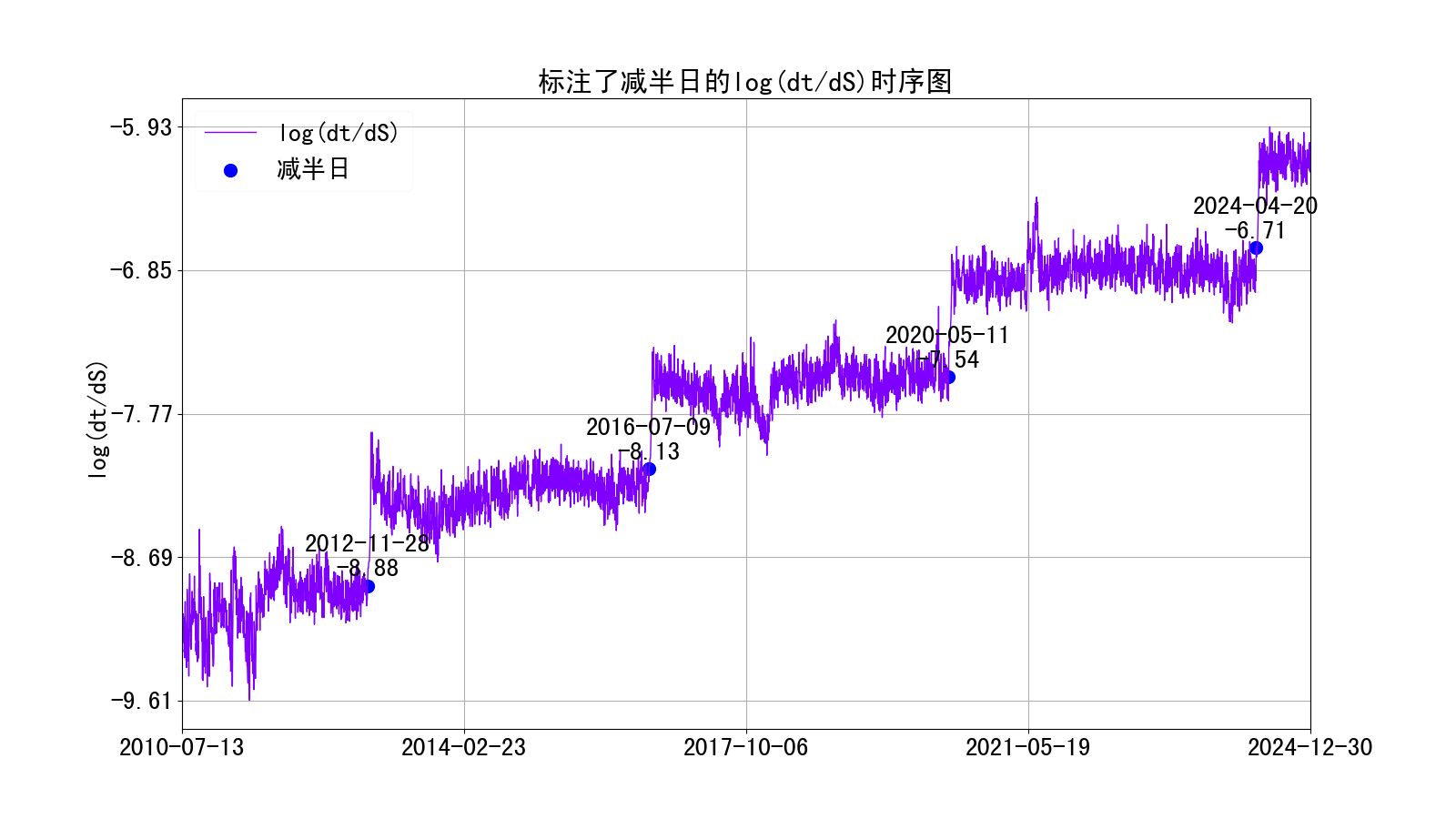
可见在一个减半周期内,该值大体上是在均值上下震荡,作出2024-04-20之后的数据、并画出了均值(均值为-6.16)的时序图,如下:
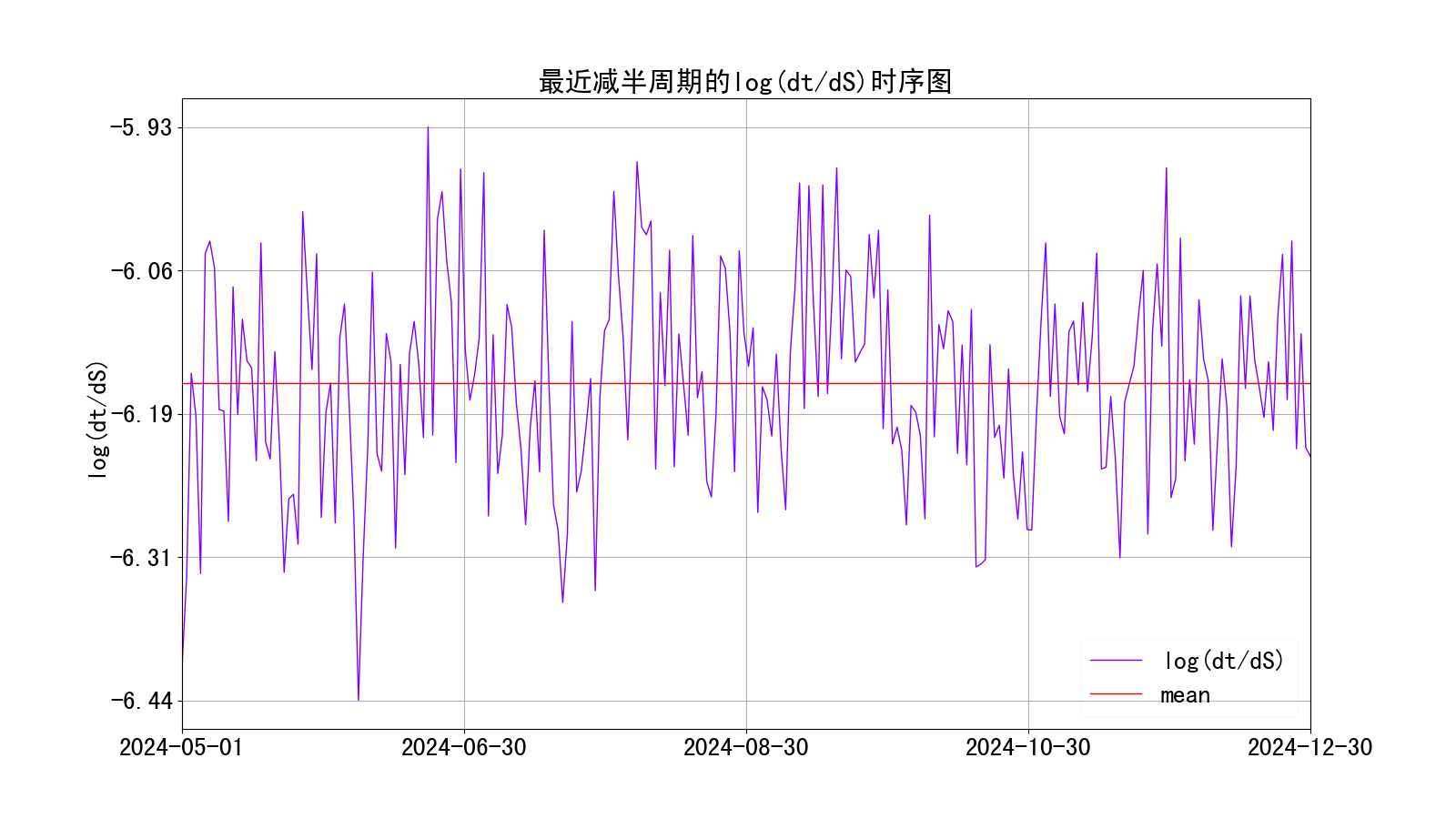
同时,还可作出产量相关项数值与比特币上线天数之间的回归图,以验证用均值来拟合这一项是否合理,如下:
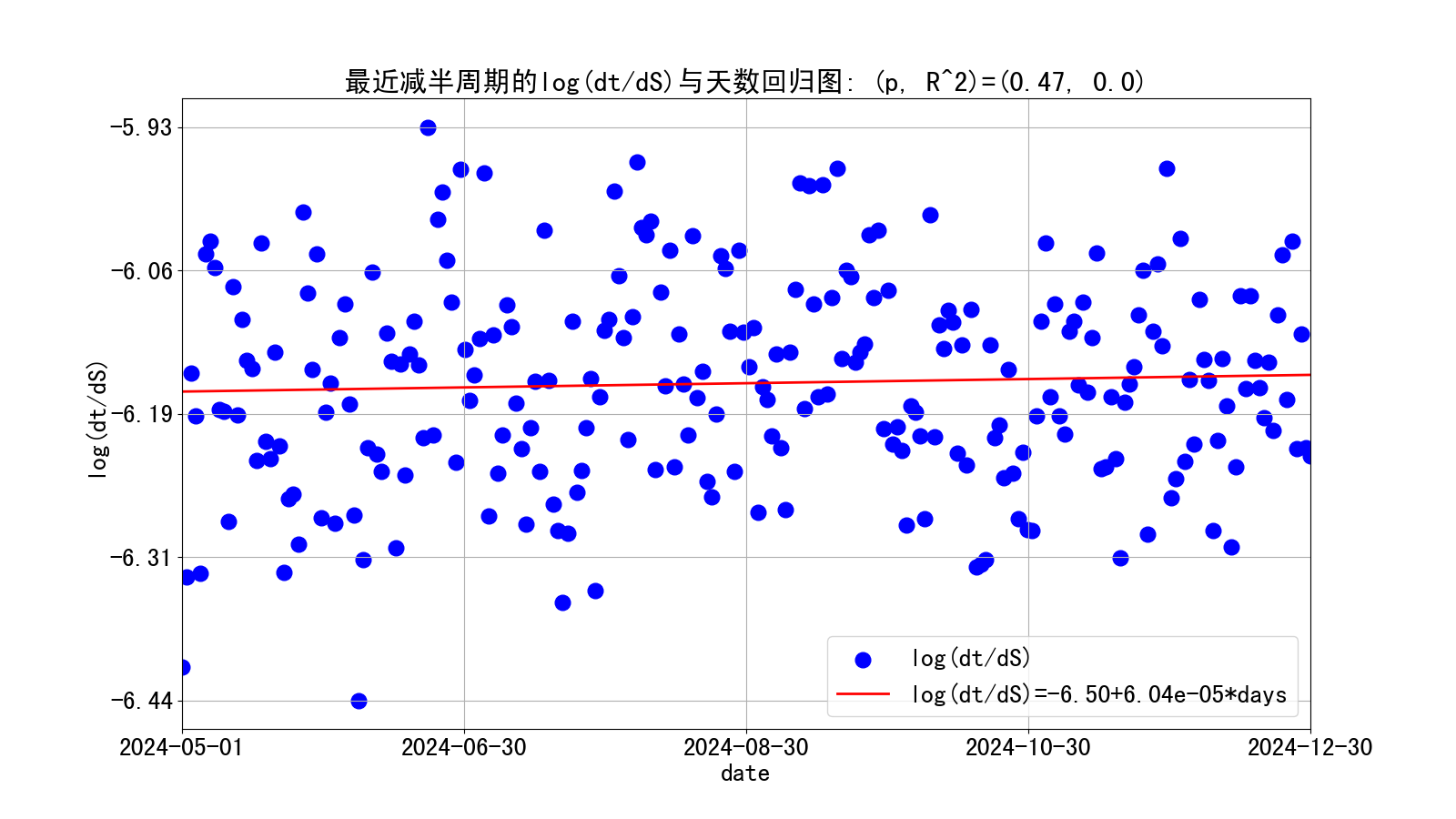
可见回归系数接近于0、且非常不显著(为0的概率很大),故可认为该项是在均值附近的白噪声。其统计情况如下:
| count 244.00 mean -6.16 std 0.09 min -6.44 25% -6.22 50% -6.16 75% -6.10 max -5.93 |
可见服从如下分布:
估计对数均衡价格时、只需要用期望值即可:
但在进行价格模拟时,该项相较于期望值的随机变化(该变化服从分布)、也会对价格波动范围产生影响、可以考虑进去。
至此,价格模型只剩下残差项了。该项具有随机性,在每个减半周期内呈现出一定的周期变化,波动范围呈现出减小的趋势。我们先对各减半周期的残差进行统计分析,统计汇总表如下:
| 周期1 周期2 周期3 周期4 周期5 count 869.00 1319.00 1402.00 1440.00 255.00 mean -0.22 0.19 -0.13 0.10 -0.09 std 0.77 0.98 0.60 0.52 0.18 min -2.24 -1.10 -1.21 -0.79 -0.46 25% -0.83 -0.73 -0.61 -0.32 -0.23 50% -0.20 -0.15 -0.15 -0.03 -0.12 75% 0.29 1.08 0.22 0.52 0.04 max 2.33 2.64 1.86 1.23 0.31 |
上表除了周期5是未完成周期之外,其余均为已完结周期。没有明显规律,不能直接用上表对周期5的残差建模,但是可以利用上表统计结果、对残差模拟值进行过滤。对不符合上表中均值、标准差的残差随机数进行过滤。即,符合预期的残差大概应该满足如下条件:为了找到残差的规律,我们先计算残差差分值,如下:即用当前时刻的残差减去上一个时刻的残差,所得残差差分时序图如下:
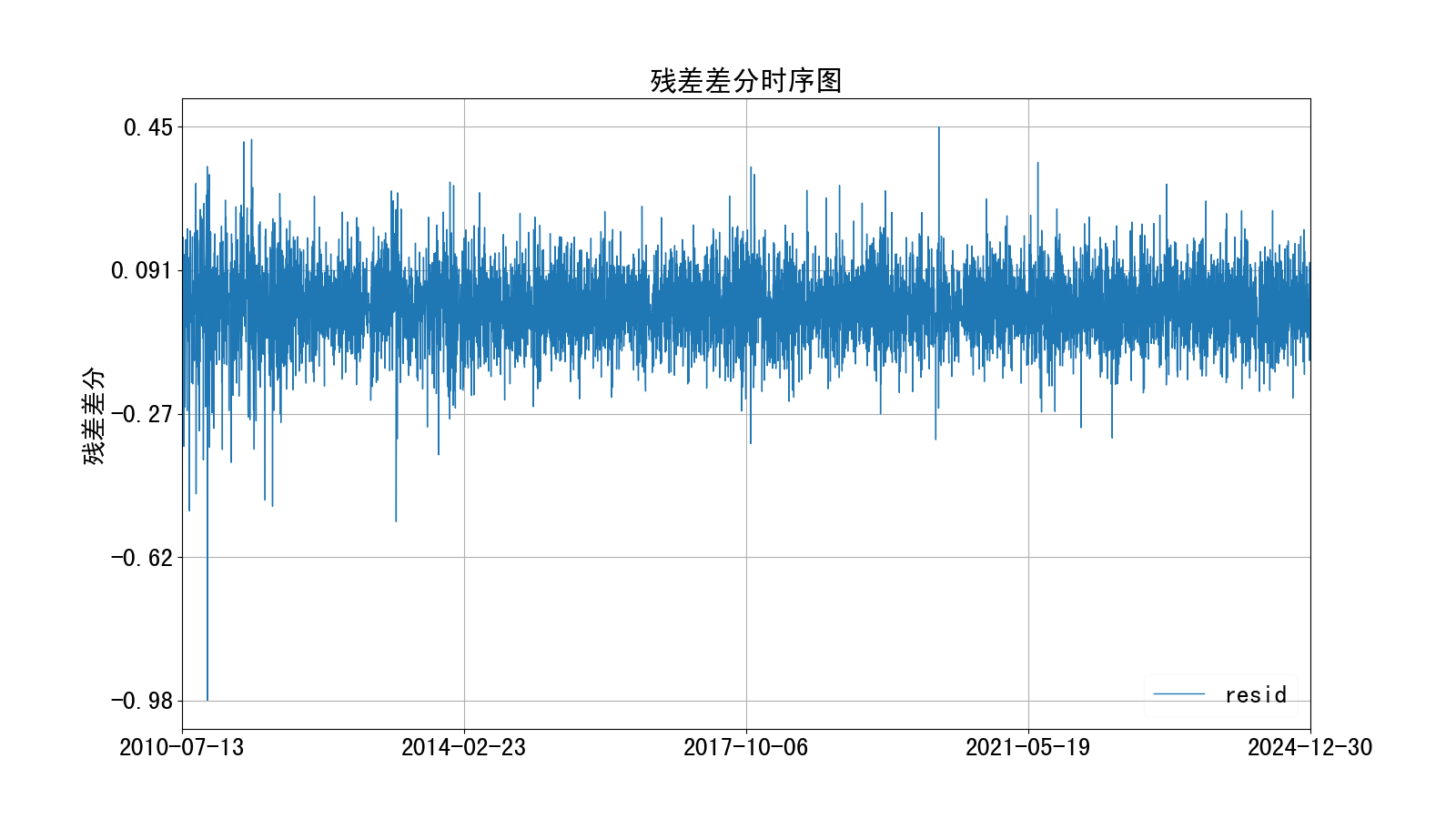
由上图可见全时序的残差差分具有非常平稳的特征,可以将其推广到未完结的周期5。上图残差差分的统计值如下:
| count 5284.0000 mean 0.0001 std 0.0953 min -0.9808 25% -0.0595 50% 0.0006 75% 0.0603 max 0.4483 |
可见均值非常接近0、标准差为0.0953,这意味着我们的残差差分值服从如下正态分布:利用上述正态分布生成后累加、可以得到任意时刻的残差模拟值。
或许有朋友会质疑,资产价格等数据在进行对数差分后、是不是都会变成与上图类似的平稳时间序列图。即如果我们直接计算比特币的对数价格差(也称为对数收益率),是否也会得到如上图所示的平稳时间序列?如果这样,那模型的意义就值得怀疑了。
为了进一步说明模型的意义,作出对数价格差的时序图,如下:

可见,对数价格差时序图明显不如残差差分时序图平稳,这意味着BTC对数价格中是存在额外信息的。通过上文所述模型,最后可以获得更好的近乎白噪声的残差差分值,说明蕴含潜在规律的信息被很大程度的包含进了模型之中。
至此,已经得到了可以对第5个减半周期价格预测和模拟的所有自变量模型。
价格预测与模拟
首先,我们考虑没有残差项的模型价格,这反映的是比特币未来一个周期的均衡价格。对数价格的效果如下:
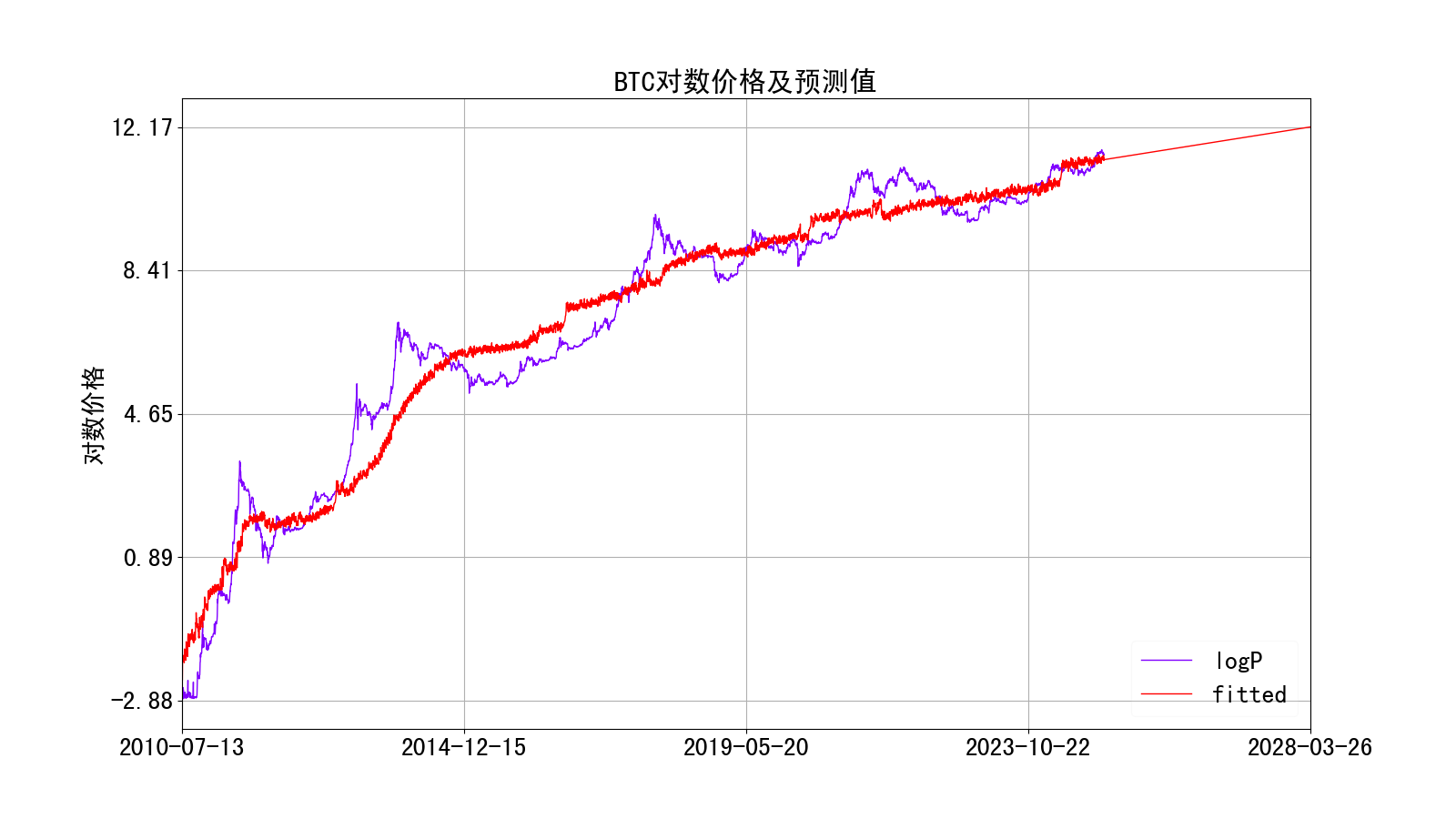
将y轴转换为原始价格(单位USD)后的预测效果如下:
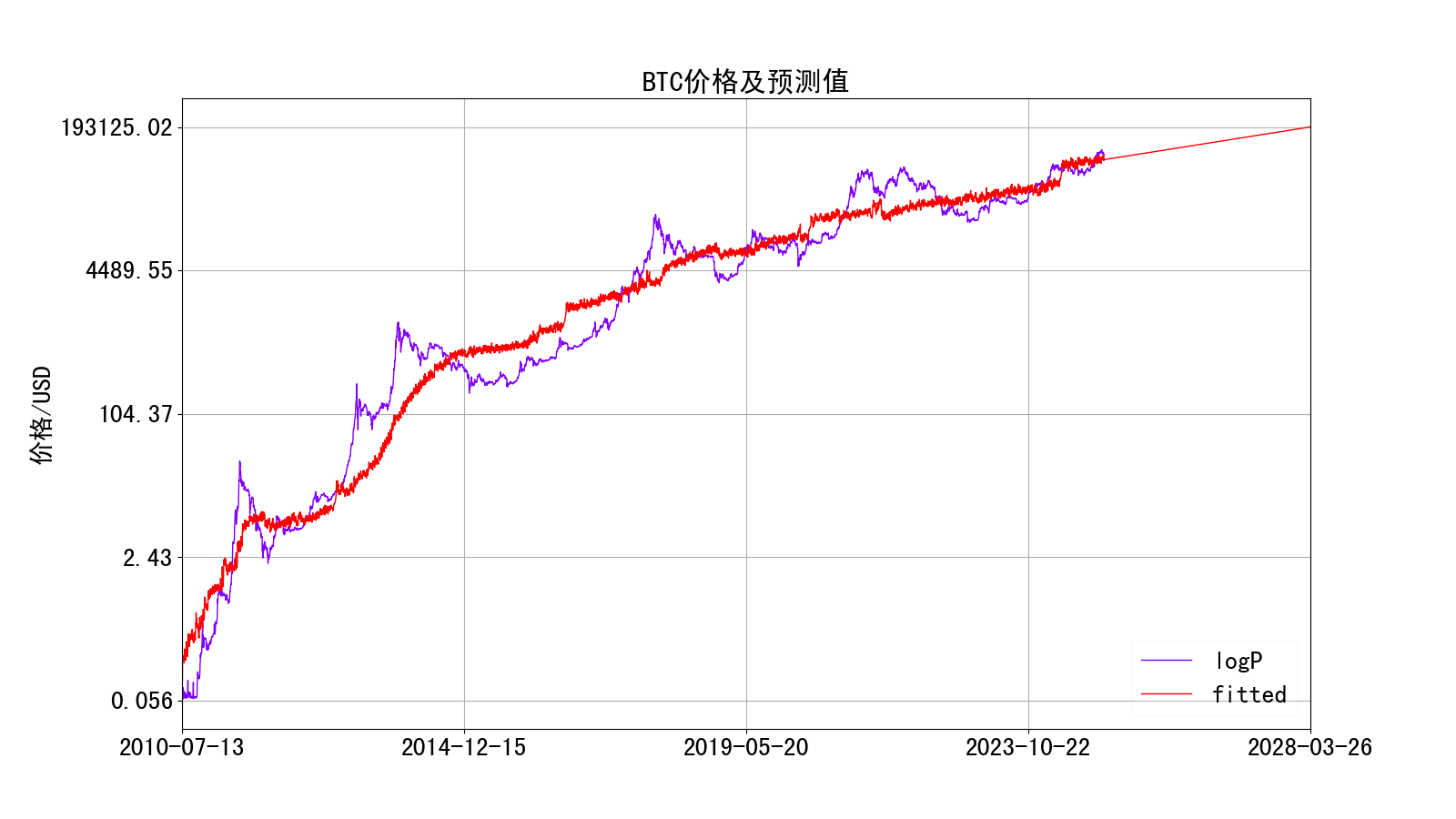
如上可见,在下次减半时、对自变量建模后的均衡价格预测值达到左右,目前(2024-12-30)的均衡价格在左右。
值的指出的是:
- 上述预测价格受到难度模型的影响,该模型忽略了因未来难度波动而偏离线性模型的可能性,且该线性回归过程包含了大量上一减半周期的数据(对应2022.01.01-2024.04.20之间的数据),这部分数据可能会影响减半(2024.04.20)后的线性回归效果,从而产生预测误差;
- 在对产量相关项()建模时,将该项的随机波动成分忽略、直接采用的减半后均值来进行预估,这也可能带来预测误差;
- 目前所得的均衡价格模型参数是通过全量数据回归所得,随着未来行情波动,该回归系数难免会失真,这也必然会导致预测出现偏差。
最后,将残差项及产量项随机性加入,仍采用上面的自变量模型、来模拟有随机涨落的未来价格。
我们分别生成服从和、长度为1182(对应预测天数)的两列随机数序列,第一列随机数累加后的残差模拟值序列需要满足条件。得到符合预期的残差序列后,将两列随机数与模型其他自变量估计值叠加,即可得到未来价格的模拟值。
某一次随机模拟的效果如下:
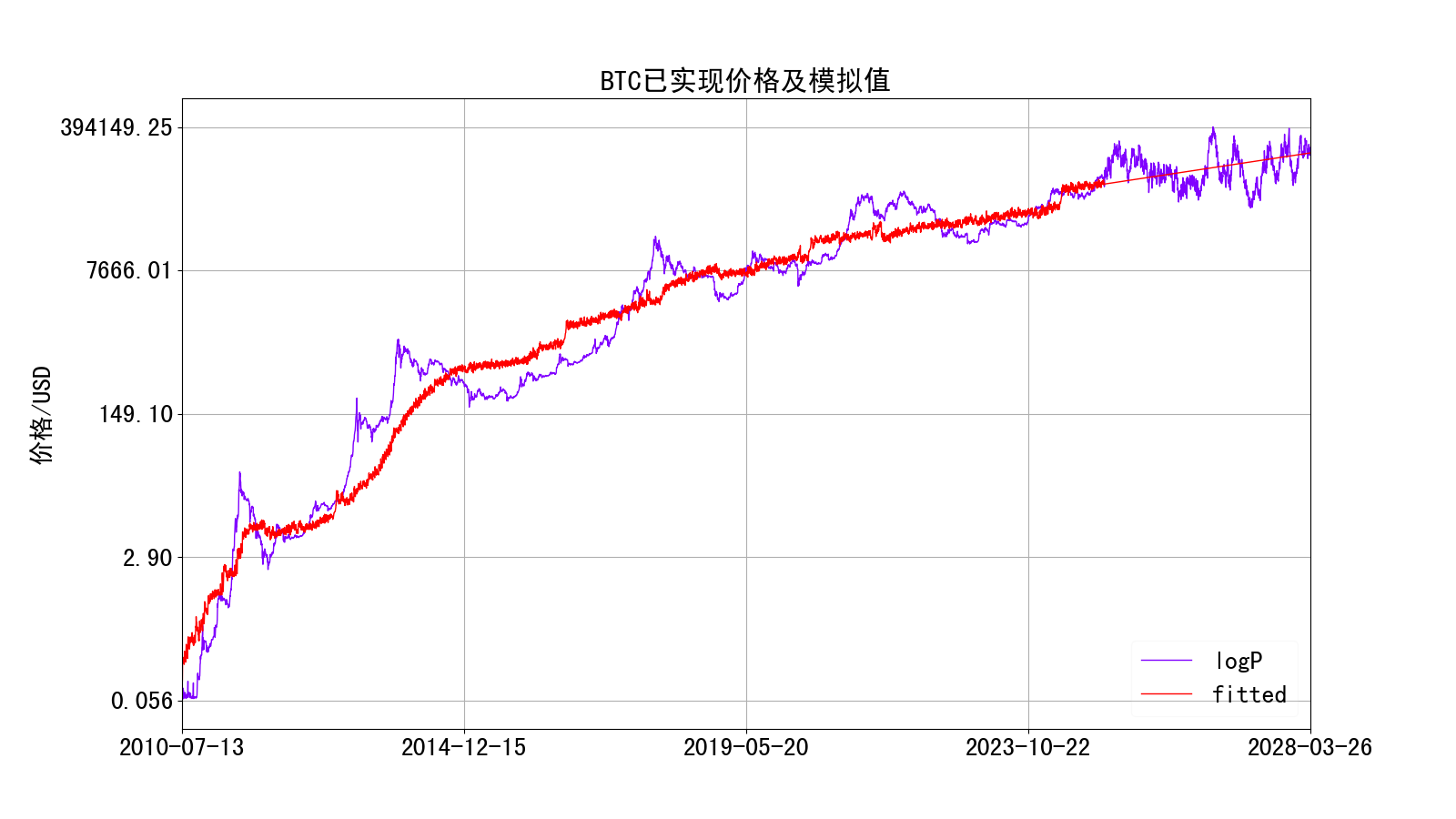
由以上模拟可见,虽然均衡价格在以下,但由于随机项的影响,价格可能会在未来一个周期内上涨至30万美元以上。
不过,该模拟结果会因为每次生成的随机数序列不同而不同,只可用于生成、展示符合模型预期的BTC随机价格、不能直接用于预测价格。
总结
本文首先对BTC均衡价格模型进行了自变量建模,进而利用自变量模型、对未来一个周期的均衡价格进行了预测,最后叠加残差等随机项、进行了符合模型预期的BTC未来价格随机模拟。
声明
本文所有观点或结论只作为研究成果展示,不作为投资建议,望读者自行斟酌!