与机器学习中MLE和MAP两大学派的对应关系
- 频率学派 – Frequentist – Maximum Likelihood Estimation (MLE,最大似然估计)
- 贝叶斯学派 – Bayesian – Maximum A Posteriori (MAP,最大后验估计)
频率论和贝叶斯方法
对于不确定性的度量统计学里至少有两种不同的考虑方式,这导致了两种不同类型的推理/决策方法,我们称之为频率论(frequentist)和贝叶斯方法(Bayesian methods)。
| Frequentist | Bayesian |
|---|---|
| 频率论方法通过大量独立实验将概率解释为统计均值(大数定律) | 贝叶斯方法则将概率解释为信念度(degree of belief)(不需要大量的实验) |
| 频率学派把未知参数看作普通变量(固定值),把样本看作随机变量 | 贝叶斯学派把一切变量看作随机变量 |
| 频率论仅仅利用抽样数据 | 贝叶斯论善于利用过去的知识和抽样数据 |
频率学派与贝叶斯学派的最主要区别:是否允许先验概率分布的使用
- 频率学派不假设任何的先验知识,不参照过去的经验,只按照当前已有的数据进行概率推断
- 贝叶斯学派会假设先验知识的存在,然后再用采样逐渐修改先验知识并逼近真实知识
因此贝叶斯推论中前一次得到的后验概率分布可以作为后一次的先验概率。但实际上,在数据量趋近无穷时,频率学派和贝叶斯学派得到的结果是一样的,也就是说频率方法是贝叶斯方法的极限。
当考虑的试验次数非常少的时候,贝叶斯方法的解释非常有用。此外,贝叶斯理论将我们对于随机过程的先验知识纳入考虑,当我们获得的数据越来越多的时候,这个先验的概率分布就会被更新到后验分布中。
频率论和贝叶斯方法各有其优劣
频率派的优点则是没有假设一个先验分布,因此更加客观,也更加无偏,在一些保守的领域比如制药业、法律比贝叶斯方法更受到信任。并且频率论方法比贝叶斯方法更容易实施,然而却更难解释。
贝叶斯派因为所有的参数都是随机变量,都有分布,因此可以使用一些基于采样的方法如MCMC方法(Markov Chain Monte Carlo))使得我们更容易构建复杂模型。
两大学派的争论
抽象一点来讲,频率学派和贝叶斯学派对世界的认知有本质不同:频率学派认为世界是确定的,有一个本体,这个本体的真值是不变的,我们的目标就是要找到这个真值或真值所在的范围;而贝叶斯学派认为世界是不确定的,人们对世界先有一个预判,而后通过观测数据对这个预判做调整,我们的目标是要找到最优的描述这个世界的概率分布。
在对事物建模时,用θ表示模型的参数,请注意,解决问题的本质就是求θ。那么:
一、频率论方法:使用简单的z-test开始假设检验
统计假设检验允许我们在数据不完整的情况下做出决策,当然从定义上说,这些决策是不确定的。统计学家已经制定了严格的方法来评估这种风险。然而,在进行决策的过程中总会涉及一些主观性。理论只是在不确定的世界中帮助我们进行决策的一种工具。
在进行假设检验时许多频率论的方法大致上包含以下步骤:
1、 写出假设,尤其是零假设(Null hypothesis),它与我们要(以一定的置信度)证明的假设相反。
2、 计算检验统计量,这是一个数学公式,取决于检验的类型,模型,假设和数据。
3、 使用计算出的值接受假设,或者拒绝假设,或者未能得出结论。
频率学派:存在唯一真值θ。举一个简单直观的例子—抛硬币,我们用P(head)来表示硬币的bias。抛一枚硬币100次,有20次正面朝上,要估计抛硬币正面朝上的bias P(head)=θ。在频率学派来看,θ= 20 / 100 = 0.2,很直观。
当数据量趋于无穷时,这种方法能给出精准的估计;然而缺乏数据时则可能产生严重的偏差。例如,对于一枚均匀硬币,即θ= 0.5,抛掷5次,出现5次正面 (这种情况出现的概率是1/2^5=3.125%),频率学派会直接估计这枚硬币θ= 1,出现严重错误。
二、使用贝叶斯方法
基于贝叶斯理论的方法主要思想是将未知参数当作是随机变量,就像描述试验时使用的变量一样。关于参数的先验知识被集成到模型中,随着观察到的数据越来越多,这些知识会被一直更新。
频率论方法和贝叶斯方法对于概率的解释不太一样。频率论认为概率是当样本的数量趋近于无穷时(样本出现)频率的极限。贝叶斯方法将其解释为一种信念(belief),它将会随着观测数据的增加而不断被更新。
这里,我们将使用贝叶斯方法重新进行之前的硬币抛掷实验。
具体做法:我们将P(head)定义为观察到硬币正面的概率。在上一节中P(head)只是一个固定的数字,然而此处我们将其看作是一个随机变量。最初,这个变量遵循一种称之为先验分布(prior distribution)的分布,它代表了在开始进行抛掷硬币之前我们对于P(head)的知识。我们将会在每次试验之后更新这个分布(后验分布,posterior distribution)。
贝叶斯学派: θ是一个随机变量,符合一定的概率分布。在贝叶斯学派里有两大输入和一大输出,输入是先验 (prior)和似然 (likelihood),输出是后验 (posterior)。
先验,即P(θ),指的是在没有观测到任何数据时对θ的预先判断,例如给我一个硬币,一种可行的先验是认为这个硬币有很大的概率是均匀的,有较小的概率是是不均匀的;似然,即P(X|θ),是假设θ已知后我们观察到的数据应该是什么样子的;后验,即P(θ|X),是最终的参数分布。
贝叶斯估计的基础是贝叶斯公式,如下:

同样是抛硬币的例子,对一枚均匀硬币抛5次得到5次正面,如果先验认为大概率下这个硬币是均匀的 (例如最大值取在0.5处的Beta分布),那么P(head),即P(θ|X),是一个distribution,最大值会介于0.5~1之间,而不是武断的θ= 1。
这里有两点值得注意的地方:
1、 随着数据量的增加,参数分布会越来越向数据靠拢,先验的影响力会越来越小
2、 如果先验是uniform distribution,则贝叶斯方法等价于频率方法。因为直观上来讲,先验是uniform distribution本质上表示对事物没有任何预判。
贝叶斯工作原理
贝叶斯定理:使用一个数学模型来对数据进行解释是数据科学中非常通用的一个想法,这被定义为一个单向的过程:model → data。一旦这个模型被确定,数据科学家的任务就变为利用数据恢复关于该模型的信息。换句话说,我们想对原始的过程进行反转:data → model。
在一个概率集合中,上述正向的过程被表示为一个条件概率:

这是模型被完全指定后观测数据出现的概率。与此相同的,反向的过程也可以表示为一个条件概率:

这在得到观测数据(我们进行试验后可以得到的数据)后提供了关于(我们正在寻找的)模型的信息。
贝叶斯定理是对概率过程model → data进行反转的通用框架的核心。它可以被定义为:

当我们得到了观测数据后,这个公式提供了关于模型的信息。贝叶斯公式被广泛的应用于信号处理,统计,机器学习,反向问题(inverse problems)和许多其他的科学应用。
在贝叶斯公式中,P(model)反映了我们对于模型的先验知识。
P(data)是数据的分布,它通常被描述为对下列式子的积分:

总之来说,贝叶斯公式为我们提供了一个关于数据推断的通用路线图:
1、 为正向过程(数据推理过程)指定一个数学模型model → data;
2、 为模型指定先验知识P(model);
3、 为求解公式进行分析或者数值运算。
计算后验分布
在这个例子中,我们可以通过贝叶斯定理得到后验分布服从下面的公式:

由于 �� 是相互独立的,因此我们可以得到(h是正面向上的次数):
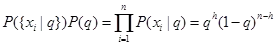
此外,我们可以分析计算如下积分(使用分部积分推导):

最终,我们将得到:

对后验概率进行最大估计
我们可以从后验分布中进行点估计。例如,对于这个分布中的 � 作最大后验估计(maximum a posteriori(MAP) estimation)。
这里我们可以通过对后验概率中的 � 求导进行估计,假定
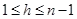
可以得到:
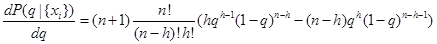
当 �=ℎ� 时,该表达式等于0,这就是对于参数 � 的最大后验估计。在这个例子中,这个值恰好是实验中正面向上出现的比例。
机器学习中的应用
一、MLE – 最大似然估计
Maximum Likelihood Estimation, 是频率学派常用的估计方法。
假设数据X1,X2,…,Xn是i.i.d.的一组抽样,X=(X1,X2,…,Xn)。(其中i.i.d.表示Independent and identical distribution,独立同分布)。那么MLE对θ的估计方法可以如下推导:

最后这一行所优化的函数被称为Negative Log Likelihood (NLL)。
我们经常在不经意间使用MLE,例如:
- 关于频率学派求硬币概率的例子,其方法其实本质是由优化NLL得出。
- 给定一些数据,求对应的高斯分布时,我们经常会算这些数据点的均值和方差然后带入到高斯分布的公式,其理论依据是优化NLL。
- 深度学习做分类任务时所用的cross entropy loss,其本质也是MLE。
二、MAP – 最大后验估计
Maximum A Posteriori, MAP是贝叶斯学派常用的估计方法。
同样的,假设数据X1,X2,…,Xn是i.i.d.的一组抽样,X=(X1,X2,…,Xn) 。那么MAP对θ的估计方法可以如下推导:
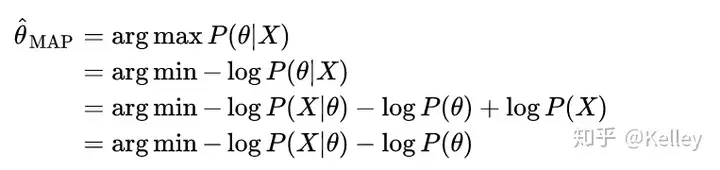
其中,第二行到第三行使用了贝叶斯定理,第三行到第四行P(X)可以丢掉因为与θ无关。
注意-log P(X|θ)其实就是NLL,所以MLE和MAP在优化时的不同就是在于先验项-log P(θ)。那现在我们来研究一下这个先验项,假定先验是一个高斯分布,即

那么,

至此,一件神奇的事情发生了 — 在MAP中使用一个高斯分布的先验等价于在MLE中采用L2的regularization。
参考资料:
https://www.cnblogs.com/chaosimple/p/4154009.html
https://www.sohu.com/a/215176689_610300